Exercise 2-20(2)
Given the assertions the interior of this wiring diagram:
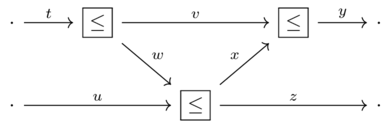
Prove that the conclusion follows using the rules of symmetric monoidal preorders
Make sure to use reflexivity and transitivity
How do you know that symmetry axiom does not need to be invoked?
Solution(1)
Assertions:
\(t \leq v+w\)
\(w+u \leq x+z\)
\(v+x \leq y\)
Conclusion: \(t+u \leq y+z\)
Proof:
\((t)+(u) \leq (v+w)+(u)\) - from monotonicity and reflexivity of u
\(= v+(w+u)\) - associativity
\(\leq v+(x+z)\) - monotonicity and reflexivity of v
\(= (v+x)+z\) - associativity
\(\leq y+z\) - monotonicity and reflexivity of z
Symmetry was not needed because the diagram had no crossing wires.